История Науки | Древнейшие определения размеров земли

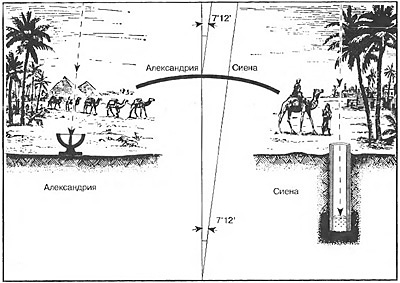
Развитие методов астрономических исследований. Вып.8, Москва-Ленинград, 1979

А.В. Клименко

Древнейшие определения размеров земли

Одной из наиболее сложных и малоисследованных проблем истории астрономии и геодезии является установление происхождения и точности результатов древнейших определений размеров Земли. Древнейшим из сохранившихся источников, в котором приводится результат определения размеров Земли, является труд древнегреческого ученого Аристотеля (384—322 гг. до к. э.) «О небе». «Математики, — писал Аристотель, — пытающиеся вычислить длину земной окружности, называют цифру около 400 000 стадиев» [1, с. 72]. Некоторые исследователи считают, что «Аристотель довольно беззаботно берет эту цифру у «математиков», не объясняя, каким образом она была выведена» [2]. Однако, более вероятно, что Аристотель и не знал, как был получен этот результат.

А.Б. Дитмар пишет, что «при вычислении размеров Земли получились явно завышенные результаты: даже если исходить из обычного стадия в 157,5 м, то окружность в 400 000 стадиев будет равна 63 000 км (вместо 40 009 км по меридиану); если же принять стадий в 176 м, то получим окружность в 70 400 км» [3, с. 40—41].

Почему же античные ученые, сообщая о третьем по счету результате определения в III в. до н. э. длины окружности Земли в 250 000 стадиев, никогда не забывали отметить, что он получен Эратосфеном, а имена авторов более ранних определений — замалчивались? Очевидно потому, что эти измерения были выполнены не греческими, а восточными, т. е. египетскими, или же вавилонскими учеными.

Традиция принижения заслуг египетских и вавилонских ученых в развитии научных знаний уходит в далекое прошлое. Так, например, один из античных писателей созданную древнеегипетскими учеными Гелиопольскую астрономическую обсерваторию близ Каира, без всяких оснований называет «евдоксовой» [1, с. 175]. Однако известно, что эта обсерватория, в которой Евдокс всего лишь «обучался астрономии» [4, с. 158] и «определял движения некоторых светил» [1, с. 175], была создана древнеегипетскими учеными. Об этом свидетельствуют следующие слова Страбона: «В Гелиополе мы видели большие дома, в которых жили жрецы, потому что, как говорят, город этот был в древности главным местопребыванием жрецов, философов и астрономов» [1, с. 174].

Греческие ученые, как правило, не указывали на источник своих научных знаний. Основную причину такого замалчивания следует искать, прежде всего в том, что для греков любой чужеземец, даже свободный представитель независимой страны, был «варваром», т. е. потенциальным рабом. На приобретенные в других странах результаты научных трудов смотрели как на свою собственность. В пораженном рабовладельческой психологией обществе не было принято ссылаться на труды «варваров».

Известно, что к 747 г. до н. э. относится начало так называемой «астрономической эры Набонассара», в течение которой в Вавилонии вели весьма интенсивные астрономические наблюдения. Греческие ученые очень высоко оценивали результаты астрономических наблюдений вавилонских жрецов. Гипсикл (III в. до н, э.), Гиппарх (II в. до н. э.) и другие греческие астрономы широко пользовались результатами вавилонских наблюдений. Даже Клавдий Птолемей во II в. н. э. пользовался ими, по существу, без всяких поправок.

Диоген Лаэрций, Страбон, Плиний и другие древние авторы писали, что многие греческие ученые обязаны своими знаниями вавилонским и египетским жрецам.

Плутарх утверждал, что научные взгляды Фалеса и других греческих ученых опирались на достижения вавилонян и египтян. Так, например, по дошедшим до нас сведениям, Фалес предсказал солнечное затмение 28 мая 585 года до н. э. Так как греки в то время еще не занимались теоретическими исследованиями в области астрономии и не вели систематических наблюдений небесных светил, то можно сделать вывод, что предсказать солнечное затмение Фалес мог лишь на основании научных достижений ученых Вавилонии и Египта. Чалоян В. К. справедливо отмечает, что «Фалес перенес из Египта в Элладу не только материалистический принцип философии — представление о воде как о начале всего сущего, но также знания по геометрии и астрономии» [5].

Существует легенда, что Пифагор первым из греческих ученых высказал идею о шарообразности Земли. Неизвестно, однако, сам он пришел к этой идее, или же, что вероятнее, заимствовал ее у своих учителей — вавилонских и египетских жрецов. Известно, что во время своего пребывания в Гелиополе, Пифагор долго учился у египетского астронома Ониуфиса. «Отличаясь по части знания небесных явлений, — писал Страбон, — жрецы держали его в тайне, неохотно вступали в общение с людьми, так что требовалось время и угодливость со стороны лиц, желавших чему-либо от них научиться; впрочем большую часть сведений варвары скрывали. Между прочим, они научили пополнять год остающимися частями дня и ночи сверх 365 дней. Тем не менее протяжение года, как и многое другое, оставалось для эллинов неизвестным до тех пор, пока позднейшие астрономы не получили этих сведений от лиц, которые перевели сочинения жрецов па греческий язык; и до настоящего времени эллины многое заимствуют у египетских жрецов и у халдеев» [1, с. 174].

О том, что в долине Нила еще в XXIX в. до н. э. вели инструментальные астрономические наблюдения, свидетельствуют результаты обследования древнеегипетских пирамид. Проверка высокоточными геодезическими методами показала [6], что истинный азимут западной стороны пирамиды Хеопса составляет в настоящее время 359°57'30". Приблизительно с такой же точностью ориентированы и другие египетские пирамиды. Очевидно, что понятие «полуденной линии» (меридиана) было известно жрецам, закрепившим на местности углы этого сооружения.

Ю. Францов приводит доказательства того, что к идее шарообразности Земли египтяне пришли значительно раньше греков. Так, в Лейденском демотическом папирусе Богиня Солнца говорит: «Смотри, Земля передо мной, как коробка; это значит, что земли бога передо мною, как круглый мяч» [7]. Но если египтяне знали о том, что Земля имеет шарообразную форму, то при достаточно высоком уровне развития у них астрономии и геометрии, они могли, как впоследствии и греки, придти к определению ее размеров. В древнеегипетских текстах действительно утверждается, что Тот (Гермес)—«бог, измеривший эту Землю», «исчисливший Землю», «сосчитавший звезды» и т. п. [8, с. 47 и 169].

Возможно, что Пифагору были известны результаты определения размеров Земли восточными учеными. Но так как сама идея шарообразности Земли в то время могла показаться абсурдной, то и не было смысла приводить длину ее окружности. Античные ученые обычно приводили значения известной им длины окружности Земли в стадиях. Однако, в арабских источниках IX—XI в. н. э. сохранились результаты древних определений размеров Земли, выраженные в вавилонской, сирийской и других системах мер длины. Некоторые из этих результатов приводятся в трудах ал-Баттани (ок. 852—926 гг.), ал-Масуди (кон. IX в. — 957 г.) и других восточных ученых. Выдающийся ученый средних веков Абу Райхан Беруни (973—1048 гг.), уделявший истории геодезии и астрономии много внимания, не мог установить размеры Земли на основании лишь сведений более ранних источников, так как, по его словам, «значение понятия «стадий» неизвестно в тех величинах, которыми мы пользуемся» [9, с. 84]. Беруни приводит результат определения длины окружности Земли, который арабские ученые «по традиции» приписывали легендарному древнеегипетскому мудрецу Гермесу. Этот результат, по словам Беруни, был равен «9 000 фарсахов при том, что фарсах — 12 000 локтей» [10, с. 210]. Наиболее вероятно, что «фарсах», которым пользовался «Гермес», был основан на «локте» в 37, 0413 см:

0,370413 X 12 000 = 4444,96 м.

В этом случае длина окружности Земли, соответствующая 9 000 фарсахам, в переводе на метрическую систему мер будет равняться

4,44496 X 9000 = 40 005 км.

Далее Беруни пишет: «В соответствии же со словами Гермеса (один градус будет равным) 25 фарсахам, что составляет 75 миль, каждая из которых равна четырем тысячам локтей» [10, с. 210]. Арабские ученые Йакут и аль-Идриси также приняли «мнение лучших авторов», по которому земной градус содержит 25 фарсахов, считая фарсах в 3 мили или 12 000 локтей [11]. Анализ этих данных показывает, что арабские ученые, не зная фактической длины фарсаха «Гермеса», сочли, что речь идет о системе мер, унаследованной арабами от персов. В этой системе мер длина локтя соответствовала 49,3884 см [12], «обычный» фарсах равнялся 5926,61 м (0,493884X 12 000), а миля — 1975,54 м. Поэтому длину окружности Земли, в переводе на метрическую систему мер, они получили равной 53 339 км (5,9261 X 9 000).

В трудах арабских ученых средних веков имеются и некоторые другие, приписываемые Гермесу, результаты определения длины окружности Земли. Так, Идриси (1100—1165 гг.) писал, что в градусе экватора Гермес установил 100 миль, что соответствует окружности Земли в 36 000 миль [13, с. 412—419]. Беруни также сообщает [10, с. 210], что «некий ученый» определил каждый градус в 100 миль, благодаря чему окружность Земли получилась равной 12 000 фарсахов.

Несомненно, что эти цифры представляют собой не какие-то независимые определения длины окружности Земли, а всего лишь интерпретацию результата, равного 9 000 фарсахов. Если результат в 36 000 миль выразить в римских милях, то получим длину окружности Земли, равную 53 340 км. Принимая «короткий» фарсах, найдем:

4,44496 X 12 000=53 339 км.

Так как длина градуса меридиана, по сообщениям Беруни, составляла 75 миль, то длина всей окружности Земли составляет 27 000 миль. Если это значение было выражено в римских милях, то получим

1,48165 X 27 000=40 005 км,

что соответствует результату «Гермеса» в 9 000 фарсахов. Если же в основу вычислений длины окружности Земли была положена персидская миля, равная 1,97554 км, то в этом случае значение окружности Земли, соответствующее 27 000 миль, также будет равняться 53 339 км.

8 древние века фарсах приравнивали 3 или же 4 милям [12]. Поэтому результаты, равные 27 000 и 36 000 миль, могли возникнуть следующим образом:

9 000 X 3=27 000 миль;

9 000 X 4=36 000 миль.

Результаты определения длины окружности Земли, полученные восточными учеными, Аристотель мог взять из трофейных трудов. Принимая известное в древности соотношение 1:45 между «варварским» схеном («хеннуб») и греческим стадием [14], Аристотель посчитал, что

9 000 X 45 = 405 000 стадиев,

или, как он отмечал в своих трудах, «около 400 000 стадиев».

Если же Аристотель исходил из результата определения длины окружности Земли, равного 12 000 фарсахов, то принимая известное в древности соотношение между фарсахом и греческим стадием как, 1:3373. он мог получить:

12 000 Х 33¹/₃ = 400 000 стадиев.

Второй по времени результат определения длины окружности Земли приведен в трудах Архимеда: «...некоторые пытались доказать, что она составляет приблизительно 300 000 стадиев...» [1, с. 83]. Это сообщение вызывает самые различные предположения относительно источника, которым воспользовался Архимед.

Несомненно, что это не мог быть результат, принадлежавший Эратосфену (250 000 стадиев). Вероятнее всего Архимед использовал тот же источник информации, что и Аристотель, выразив полученный восточными учеными результат в 9 000 «фарсахов» в другой метрологической системе. Наиболее вероятное объяснение происхождение результата, равного 300 000 стадиев, заключается в следующем.

Принимая известное в античный период соотношение 1:33¹/₃ между «фарсахом» и стадием, Архимед нашел значение окружности Земли, которое и приведено в его трудах: 9 000 Х 33¹/₃ = 300 000 стадиев.

Среди исследователей нет единого мнения и в оценке точности определения размеров Земли древнегреческим ученым Эратосфеном (ок. 276—194 гг. до н. э.). Достаточно отметить, что длину «стадия Эратосфена» исследователи принимают в пределах от 148 до 210 м. Большинство же авторов считают, что при определении длины окружности Земли Эратосфен принял стадий, равный) 157,5 м.

Для того, чтобы установить значение полученной Эратосфеном длины окружности Земли, важно выяснить, чему равнялись те стадии, которыми он измерял расстояние от Александрии до Сиены.

Древнегреческий историк Геродот, путешествовавший в V в. до н. э. по Египту, писал, что расстояние от устья Нила до Элефантины равняется 136 схенам или 8160 стадиев [1, с. 29]. Вовремя своего путешествия по Египту Геродот не занимался измерениями длины пройденного пути, а получал ее от местных , жителей. Затем, при обработке своих путевых заметок, расстояния, полученные в египетских схенах, он переводил в греческие стадии.

Египетский схен, по данным Геродота, состоял из 60 стадиев. Однако Страбон, Артемидор и др. древние ученые писали, что в различных частях Нила схен приравнивали 30, 40, 60, и даже 120 стадиям.

Анализ приведенных Геродотом расстояний показывает, что упоминаемый им египетский схен равнялся 40, а не 60 греческим стадиям. Если принять, что длина схена равнялась 40 стадиям (185,207 X 40 = 7408,26 метров), то расстояние между устьем Нила и Элефантиной получим весьма близким к фактическому:

136 X 40 = 5440 стадиев;

7,40826 X 136 = 0,185207 X 5 440= 1 008 км.

Расстояния между населенными пунктами долины Нила были известны египтянам еще в глубокой древности. Эти расстояния в течение многих веков неоднократно измерялись землемерами и бематистами. Встречающиеся в древних источниках различные значения таких расстояний очевидно и выражают результаты многократных измерений. Например, Плиний Старший писал, что «остров Элефантина... находится в 585 000 шагах от Александрии» [1, с. 257]. Так как геометрический шаг равнялся 1,4817 м, то указанное расстояние будет составлять 867 км. Ссылаясь на Юбе, Плиний сообщает, что от Александрии до Элефантины 562 000 шагов, что соответствует 833 км.

Артемидор считал, что от Александрии до Элефантины , 762 000 шагов (ок. 1129 км), а Аристокреонт — 750 000 шагов, что соответствует 1111 км.

Эратосфен, как известно, считал, что от Александрии до Сиены 5 000 стадиев. По данным Страбона это расстояние равняется 5 300 стадиям. Если учесть, что Элефантина находилась от Сиены в 16 000 шагах (около 130 стадиев) выше по течению Нила [1, с. 257], то ясно, что указанное Страбоном расстояние от устья этой реки до Сиены весьма близко к значению, полученному из анализа сообщений Геродота. При длине стадия в 185,207 м найдем:

5 000 X 0,185207 = 926 км;

5 300 X 0,185207 = 981 км.

Фактически же указанное расстояние (по долине Нила) равно 980 км.

Римский архитектор Витрувий (1 в. до н. э.) писал: «Эратосфен Киренский по пути Солнца, равноденственным теням гномона и склонению неба определил, на основании математических и геометрических вычислений, что окружность Земли равна 252 000 стадиев, что составляет 31 500 000 шагов» [15]. Учитывая, что древнегреческий («олимпийский») стадий был равен 185,207 м, а шаг (римский «геометрический пасс») — 1,48165 м [12], найдем длину окружности Земли, соответствующую в метрической системе мер, 252 000 стадиев или 31 500 000 шагов:

252 000 X 0,185207 = 46 672 км;

31 500 000 X 0,001481652 = 46 672 км.

Другой известный римский ученый Плиний Старший писал, что полученная Эратосфеном длина окружности Земли составляет 252000 стадиев или 31 5000 римских миль [161. Так как римская миля равнялась 1 000 геометрическим пассам, то очевидно, что

31 500 X 1,481652 = 46 672 км.

Плиний приводит [16] значение радиуса Земли, равное 42 000 стадиев, якобы связанное с именем Дионисидора. По-видимому этот результат выведен из представленной Эратосфеном длины окружности Земли, равной 252 000 стадиев. При этом отношение длины окружности к диаметру принималось равным трем, хотя еще в III веке до н. э. Архимед и Аполлоний значение числа π получили с более высокой точностью. Длина окружности Земли, равная 252 000 стадиев, приводится также в трудах римского врача и естествоиспытателя Клавдия Галена (129—ок.201 гг.).

По сообщению Клеомеда Эратосфен получил длину окружности Земли, равную 250 000 стадиев [17]. Если Эратосфен пользовался древнегреческим стадием, то полученная им длина окружности Земли составляла

250 000 X 0,185207 = 46302 км.

Даниель Барбаро (1514—1570), ссылаясь на древнеримские источники, писал, что по данным Эратосфена окружность Земли равняется «250000 стадиев, то есть 31250 милям» [18]. Из этих данных вытекает, что

31 250 X 1,481652 = 46 302 км.

Арабские авторы приводят значения окружности Земли, источник которых, несомненно, тот же, что и результата, равного 250 000 стадиев. Так, например, крупнейший математик и астроном XV века ал-Каши писал [19], что длина окружности Земли равна 7807 фарсахам. Так как «обычный» фарсах равнялся 32 древнегреческим стадиям (32X0,185207=5,92661 км), то длина окружности Земли, в переводе на метрическую систему мер, будет равна

7 807 X 5,92661 = 46 269 км,

что весьма близко к приведенному выше результату в 250 000 стадиев. Расхождение в 33 км можно объяснить округлении числа я, учитывая, что в арабских источниках [19] приводится не длина окружности Земли, а ее диаметр (5 X 497 = 2485 фарсахам).

Арабский астроном — наблюдатель ал-Баттани (ок. 852— 926) писал, что «Величина одного градуса в упомянутых милях близка к 65» [20, с. 104]. Есть основание считать, что более точная цифра приведенной ал-Баттани длины градуса большого круга Земли должна равняться 65°,1. Отсюда получим длину всей окружности Земли:

65,1 X 360 = 23 436 миль.

Так как в Арабском халифате применялась вавилонская (персидская) миля протяженностью 1,97554 км, то длина окружности Земли по этим данным будет равна 46299 км; (23436 X 1.97554), которая, практически, не отличается от приведенных в трудах античных и арабских ученых различных интерпретаций полученного Эратосфеном результата в 250 000 стадиев.

Опираясь на свидетельства Витрувия, Плиния Старшего, ал-Каши, Барбаро и других авторов, а также данные исследований в области истории метрологии, можно сделать вывод, что результаты определения Эратосфеном длины окружности Земли были основаны на древнегреческом стадии в 185,2 м.

Из древних источников известен также результат определения размеров Земли, равный 180 000 стадиев. Впервые это значение было приведено в «Географии» Страбона (1 в. до н. э. — I в. н. э.). «Из новых измерений Земли, — писал Страбон, — ...самые малые размеры — измерения Посидония, считающего окружность Земли около 180 000 стадиев» [21]. По сообщению Клавдия Птолемея (ок. 90—169 гг.), Марин Тирский «вычислил, что 1/360 часть большого круга равна на поверхности Земли 500 стадиям — цифра, отвечающая не вызывающим сомнения измерениям» (1, с. 298).

В труде Клеомеда [17] упоминается еще один результат определения длины окружности Земли, приписываемый Посидонию, — 240 000 стадиев. М. Лефранк считает [22], что цифры 180 000 и 240 000 стадиев являются одной и той же линейной величиной, но выраженной стадиями различной длины в 210 и 157,5 м. Высказанная Лефранк идея о линейном равенстве значений в 180 000 и 240 000 стадиев представляется, как будет показано ниже, весьма обоснованной, хотя исследования истории линейных мер [12] дают основание утверждать, что стадия длиной 157,5 м в античное время не существовало.

По словам Клеомеда [17], Посидоний, наблюдая на Родосе и в Александрии звезду Каноп, установил, что длина дуги на земной поверхности между этими городами составляет ¹/₄₈ часть большого круга Земли. Полагая, что расстояние между Родосом к Александрией соответствует 5 000 стадиев, Посидоний получил длину (5 000 X 48) окружности Земли, равную 240 000 стадиев.

Однако ¹/₄₈ части окружности соответствует угол, равный 7°30'. Фактическая же разность широт Родоса и Александрии составляет 5°14', т. е. около 7б9 части окружности Земли. Плиний также писал, что «для людей, смотрящих на Каноп из Александрии, он появляется над горизонтом приблизительно на четвертую часть одного знака, а на Родосе он каким-то образом соприкасается с Землей» [1, с. 244]. Так как знак зодиака (360°:12) составляет 30°, то четвертая его часть равняется 7°30'. По-видимому Посидоний и Плиний пользовались одним и тем же источником информации о разности широт Родоса и Александрии. Если бы Посидоний действительно производил астрономические наблюдения на Родосе, то вряд ли он мог бы сделать какие-либо выводы относительно высоты звезды Каноп, которая,. если следовать мнению древних авторов, даже не появлялась там над горизонтом.

Все это дает основание предполагать, что Посидоний не проводил инструментальных наблюдений звезды Каноп на Родосе, и в Александрии, а использовал для своих выводов литературные источники.

Из трудов Эратосфена известно, что в его время расстояние между Родосом и Александрией принимали равным 5 000, 4 000 или 3750 стадиев [23].

По-видимому, все указанные цифры являются одной и той же линейной величиной, выраженной стадиями различной длины:

5000 X 0,148165 = 740,83 км;

4000X0,185207=740,83 км;

3750X0,197554=740,83 км.

Придерживаясь данных Посидония, найдем вычисленное им значение окружности Земли, выраженное в метрической системе мер:

740,83 X 48 = 35560 км.

Если принять ионийский стадий, то расстояние между Родосом и Александрией будет составлять 5000 x 0,197554 = 987,77 км, а длина окружности Земли — 987,77 X 48 = 47 413 км.

Расстояние же между Родосом и Александрией равно 600 км. Следовательно, Посидоний в своих вычислениях оперировал не только преувеличенной разностью широт Родоса и Александрии, но и значительно завышенным расстоянием между указанными пунктами. Следует также учесть, что на результатах этих определений, несомненно должна была отразиться и значительная разность долгот (около 1°43') Александрии и Родоса.

Для того, чтобы установить происхождение приписываемых Посидонию результатов измерения длины дуги меридиана между Александрией и Родосом, рассмотрим некоторые другие источники, в которых сохранились фрагменты известных древним авторам результатов работ по определению размеров Земли.

Так, некоторые арабские ученые, ссылаясь на древние источники, писали [19, 24], что окружность Земли равняется 8 000 фарсахов.

Опираясь на эти данные, вычислим длину окружности Земли, соответствующую 8 000 фарсахов:

8 000 X 5,92661 = 47 413 км.

Беруни писал в одном из своих трудов: «Передают в книгах (в виде традиции), что древние ученые нашли города Ракку и Тадмор на одной и той же линии из числа полуденных, а между ними — 90 миль. Отсюда они вывели, что величина одного градуса— 662/3 мили» [10, с. 210]. Длина окружности Земли по этим данным составляет 24 000 миль.

И.Ю. Крачковский, ссылаясь на средневекового арабского ученого Иакута, пишет, что определение длины дуги одного градуса меридиана в 66²/₃ мили было выполнено «...Птолемеем на основе измерений в Верхней Месопотамии между Харраном и горами Амиды» [20, с. 84]. Вполне возможно, что в этом районе когда-либо и производились работы по определению длины дуги градуса меридиана, но не Птолемеем. В своих трудах Птолемей ссылается лишь на одну цифру — 180 000 стадиев, причем неоднократно подчеркивает, что она получена Мариной Тирским (ок. 1 в. н. э.) в результате «вычислений», а не «измерений».

Выполнение же работ по измерению длины дуги градуса меридиана между Тадмором (Пальмирой) и Раккой Крачковский относит к 827 году. Он пишет: «Для измерения была выбрана степь между Пальмирой и Раккой на Евфрате и долина в Верхней Месопотамии около Синджара между 35° и 36° северной широты. Комиссия, собравшаяся в центральном пункте, разделилась на две партии: одна отправилась на юг по линии меридиана на расстояние градуса, а другая на такое же расстояние на север. По возвращении в исходный пункт они произвели сверку полученных результатов и установили конечный вывод... Астроном конца X века Ибн Йунус передает, что одна партия определила величину градуса в 57, а другая в 56¹/₄ мили; когда результаты были представлены ал-Мамуну, он решил остановиться на средней цифре в 56²/₃ мили» [20, с. 83].

Здесь следует обратить внимание на некоторые противоречия в освещении этого события указанным источником. Во-первых, город Ракка находится в 250 км к западу от долины Синджара, где производились измерения длины дуги градуса меридиана астрономами и геодезистами ал-Мамуна. Так как обе партии, как известно, начинали измерения от общего пункта, то ясно, что они не имели отношения к градусным измерениям в районе Тадмора и Ракки. О том, что обе партии начинали измерение из одного, общего пункта, расположенного южнее Синджара, сообщает также Беруни [10, с. 210].

Во-вторых, обе геодезические партии ал-Мамуна, как видно из сохранившихся источников, измеряли дугу меридиана, равную одному градусу. Разность же широт Ракки и Тадмора составляет 1°22'.

Так как в Арабском халифате в употреблении была миля длиной 1975,54 м, то полученное в результате измерений 827 года значение дуги градуса меридиана соответствует 111 947 м.

Результат, равный 66²/₃ мили, не принадлежит и известному арабскому ученому ал-Баттани (ок. 858—929), который в 877—918 гг. вел регулярные астрономические наблюдения в Ракке. Ал-Баттани считал [20, с. 84], что длина дуги градуса меридиана равна 75 милям, а длина окружности Земли—:27 000 миль.

Важно отметить, что ошибка определения древними учеными разности широт Ракки и Тадмора, как установил еще Беруни, не превышала 1'. Однако ученые, определявшие здесь длину дуги градуса меридиана, ошиблись, полагая, что Ракка и Тадмор находятся на одном меридиане. Фактически разность долгот этих пунктов составляет около 45'.

Так как линия, связывающая Тадмор и Ракку, отклоняется от направления меридиана на величину около 24°, то ясно, что никаких инструментальных измерений расстояния здесь не производилось. Иначе разность долгот Ракки и Тадмора была бы замечена. По-видимому, расстояние между Тадмором и Раккой было установлено, как это обычно и делалось в древности, по времени движения каравана. Именно этим можно объяснить, почему вместо фактического расстояния между Тадмором и Раккой, равного 84 милям, было получено 90 миль.

По данным Тадморских измерений длина дуги градуса меридиана, в переводе на метрическую систему мер, была определена в 131,7 км (66²/₃ Х 1,97554), а окружность Земли — 24 000 X 1,97554 = 47 413 км.

Так как фарсах состоял из 3 вавилонских миль (1975,54 х 3 = 5926,61 м), то можно прийти к выводу, что значения окружности Земли, равные 8 000 фарсахов и 24 000 миль, представляют собой одну и ту же линейную величину (8 000 x 3 = 24 000), соответствующую 47 413 км, и, следовательно, являются результатом одних и тех же градусных измерений.

Полученный из Тадморских градусных измерений результат,.. равный 24 000 миль, Посидоний мог выразить более привычной для античных ученых мерой длины — стадием. Из различных источников известно, что миля состояла из 7¹/₂, 8, 8¹/₃ и 10 стадиев, т. е.

197,554 Х 7¹/₂ = 1481,65 м;

185,207 X 8 = 1481,65 м;

177,798 Х 8¹/₃ = 1481,65 м;

148,165 X 10 = 1481,65 м;

197,554 X 10 = 1975,54 м.

Исходя из того, что результаты Тадморских измерений выражены римскими милями, Посидоний мог вычислить два значения длины окружности Земли — в ионийской (24 000 Х 7¹/₂ = 180 000 стадиев) и римской (24 000 X 10 = 240 000 стадиев) метрологических системах. Таким образом, оба приписываемые Посидонию результата —180 000 и 240 000 стадиев, как и предполагала М. Лефранк, могут являться одной и той же линейной величиной:

180 000 X 0,197554 = 240 000 X 0,148165 = 35 560 км.

О том, что значения в 180 000 и 240 000 стадиев имеют именно такое происхождение, свидетельствуют и некоторые другие, более поздние источники, содержащие сведения об измерениях окружности Земли в древние века. Так, например, Наллино передает сообщение арабского географа Йакута о том, что длина окружности Земли в 24 000 миль соответствует 180 000 стадиев античных авторов [13, с. 413].

Из данного анализа вытекает, что ни Посидоний, ни Марин: Тирский не производили сами измерений длины окружности Земли. Приписываемые им данные (180 000 и 240 000 стадиев) являются интерпретацией результатов градусных измерений, выполненных в районе Тадмора и Ракки.

Возможно, что и Эратосфену сведения о методах и результатах определения размеров Земли учеными Востока стали известны из хранившихся в Александрийской библиотеке многочисленных трудов восточных ученых. Не случайно Эратосфен: написал не дошедшую до нас поэму «Гермес», куда включил обширный астрономический и географический материал [1, с. 88]. Следует обратить внимание на то, что Аристотель говорит о «математиках», пытающихся «вычислить», а не «измерить» длину окружности Земли. Однако, при определении длины окружности Земли греческие ученые не могли бы обойтись без соответствующих астрономических и геодезических измерений. Так как о подобных измерениях, выполненных до Эратосфена, никто из античных авторов не упоминает, то очевидно греки их и не производили, а использовали результаты определения размеров Земли учеными Востока.

Установление происхождения и точности древнейших определений размеров Земли поможет раскрыть направления и масштабы научных связей между центрами древних цивилизаций, осветить еще одну страницу истории астрономии и геодезии.

ЛИТЕРАТУРА

1. Античная география. Сост. М.С. Боднарский, М., 1953.

2. Томсон Дж. История древней географии. М., Географгиз, 1953, с, 174.

3. Дитмар А.Б. Рубежи ойкумены. М., «Мысль», 1973.

4. Диодор Сицилийский. Историческая библиотека, том 1. СПб., 1774.

5. Чалоян В.К. Восток-Запад (преемственность в философии античного и средневекового общества). М., «Наука», 1968, с. 47.

6. Clarke S., Engelbach R. Ancient Egyption Masonrv the Building Craft. Oxford, 1930, p. 69.

7. Францов Ю. К эволюции древнеегипетских представлений о Земле. «Вестник древней истории», 1940, № 1, с. 48.

8. Тураев Б. Бог Тот. Опыт исследования в области древнеегипетской культуры. Лейпциг, 1898.

9. Беруни. Избранные произведения, том 5, ч. 1. Ташкент, 1973.

10. Беруни. Избранные произведения, том 3. Ташкент, 1966.

11. Бериар Kappa де Во. Арабские географы. Л., 1941, с. 15.

12. Клименко А.В. Значения некоторых древних единиц линейных мер. «Вопросы геодезии, фотограмметрии и картографии», М., 1977.

13. Nailinо С. Raccolta di scritti editi e inediti, vol. 5, Roma, 1944.

14. Heгоnis A1exandrini. Opera quae supersunt omnia, vol. ÏV. Lipsiae, 1912, p. 184.

15. Витpувий. Десять книг об архитектуре. М., 1936, с. 36

16. Р1ïnius. Natural history, b. 2. London, 1947, p. 247.

17. К1eоmed «s. Die Kreisbewegung der Gestirne- Leipzig, 1927, s. 36

18. Барбаро Д. Комментарий к «Десяти книгам об архитектуре» Витрувия. М., 1938, с. 52.

19. Джемшид Гиясэддин. а л-Каш и. Трактат об окружности. М, 1966, с. 368.

20. Крачковский И.Ю. Избранные сочинения, том IV, М. — — Л., 1957.

21. Страбон. География в 17 книгах. М., 1964.

22. Leffranque M. Poseidonios dArameé. Paris, 1964.

23. Дитмap A. Б. Родосская параллель. M., 1965, с. 35.

24. Перевощиков Д. M. Историческое обозрение исследований о фигуре и величине Земли. «Магазин землеведения и путешествий», том 1, 1852.

Материалы: http://www.astro-cabinet.ru/library/Stat/Zemlja.htm